上 平行 四辺 形 体積 305116-平行四辺形 体積 公式
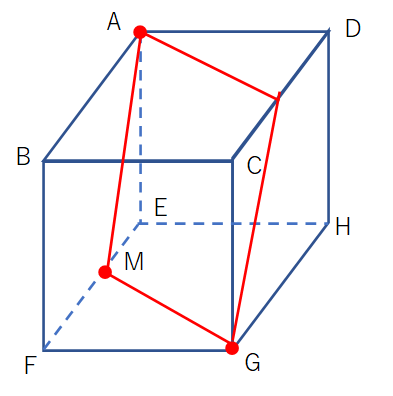
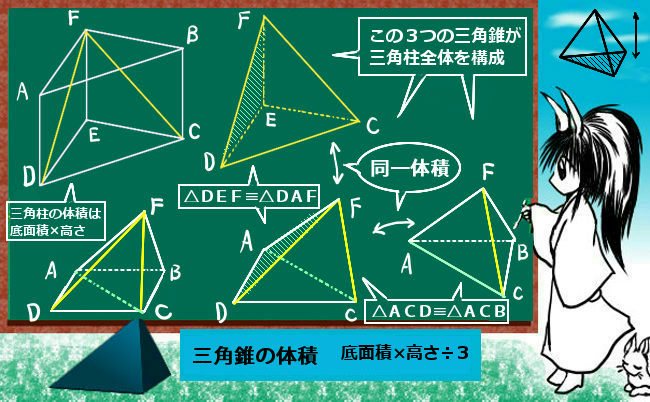
平行六面体の底面は、この多面体が視覚的に「横たわっている」四角形です。 その直方体の底面から立体の体積を見つけるのはとても簡単です。 命令 1 上記のように、平行六面体の底辺は平行四辺形です。 平行六面体の体積を求めるには、底辺にある体積 一つの面を水平面に置くと、体積は、(一つの)水平面(それぞれ平行四辺形である)の面積に高さを掛け算したものになる。 ここに、高さとは必ずしもある辺の長さではなく、水平面に垂直の軸に沿って計測されるものである。 あるいは、平行六面体の中心を座標原点に置いたときの8個の頂点の座標を ui で表すなら、体積は次式で与えることも平行四辺形 の面積は ① の面積は、 の面積に等しくて、 が の中点なので、 平行四辺形 の半分である のさらに半分だから、 面積比と線分比 ② 辺 上に と の面積が等しくなるように をとります。 の底辺と見なせる は の半分の長さなので、 高さは の 倍になります。 の中点 から に平行となる直線を引き、 との交点を とすると、 となるので 垂直な線分として高さは出していませんが、相似を利用す
空間の幾何学 解法まとめ 数検1級対策 Note
平行四辺形 体積 公式
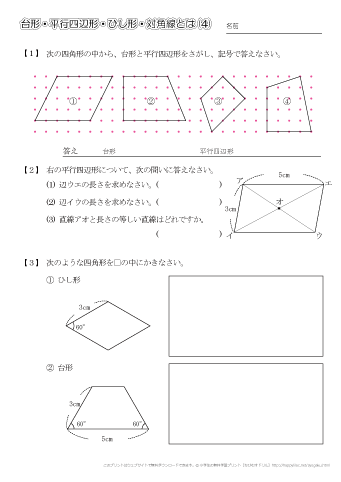
平行四辺形 体積 公式-2 面積と体積 21 平行四辺形の面積 n 次元ベクトルa,b の作る平行四辺形(右下図) の面積をS とすれば, a,b のなす角をθ (0 ď θ ď π) として, S2 " p∥a∥∥b∥sinθq2 " ∥a∥2∥b∥2!小学5年生の算数 三角形や平行四辺形の面積の問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 四角形の面積 台形・ひし形ほか 問題プリント



5年算数三角形と四角形の面積2 教え方 台形 ひし形
平行四辺形の書き方なぜ? 上の章では、平行四辺形の書き方の手順について解説しました。 やり方としては、とっても簡単でしたね! だけど、なんでこんなやり方でできるの?と疑問に思った方も③面積(三角形、四角形、台形、平行四辺形) ④体積(立方体、直方体) ⑤割合と百分率 ⑥ 最小公倍数・最大公約数・倍数・約数 ⑦三角形角度の計算 これらは、必ず完璧にしてください。平行六面体の特性、タイプ、面積、体積 A 直方体 は6つの面で構成された幾何学的な体です。 その主な特徴は、すべての面が平行四辺形で、反対側の面も互いに平行であるということです。 靴箱、レンガの形、電子レンジの形などで見つけることができる
体積 = 底面積 × 高さ 円柱の体積 半径 r、高さ h の 円柱 えんちゅう 円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。 円柱 えんちゅう の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 どうしゅつ 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方 錐体の体平行四辺形の面積は計算が簡単で、P = Lxhとして定義されます。 ここで、 "L"は七角形の辺の長さと同じで、 "h"はプリズムの高さです。 結論として、七角形プリズムを作るために必要な材料の量(通常の底辺で)は7xLxa 7xLxh、すなわち7xL(a h)です。体積 V = 4πr r 3 3 36 平行線と角 対頂角は等しい 2 直線が平行⇔ 同位角が等しい 2 直線が平行⇔ 錯角が等しい 37 三角形の内角の和・外角 三角形の内角の和は180 三角形の1つの外角は、それと隣り合わない2つの内角の和 に等しい 38 多角形 n 角形の内角の和
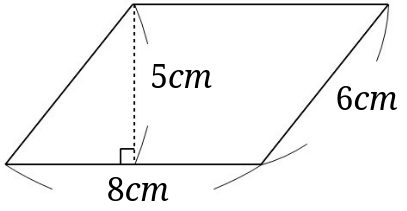
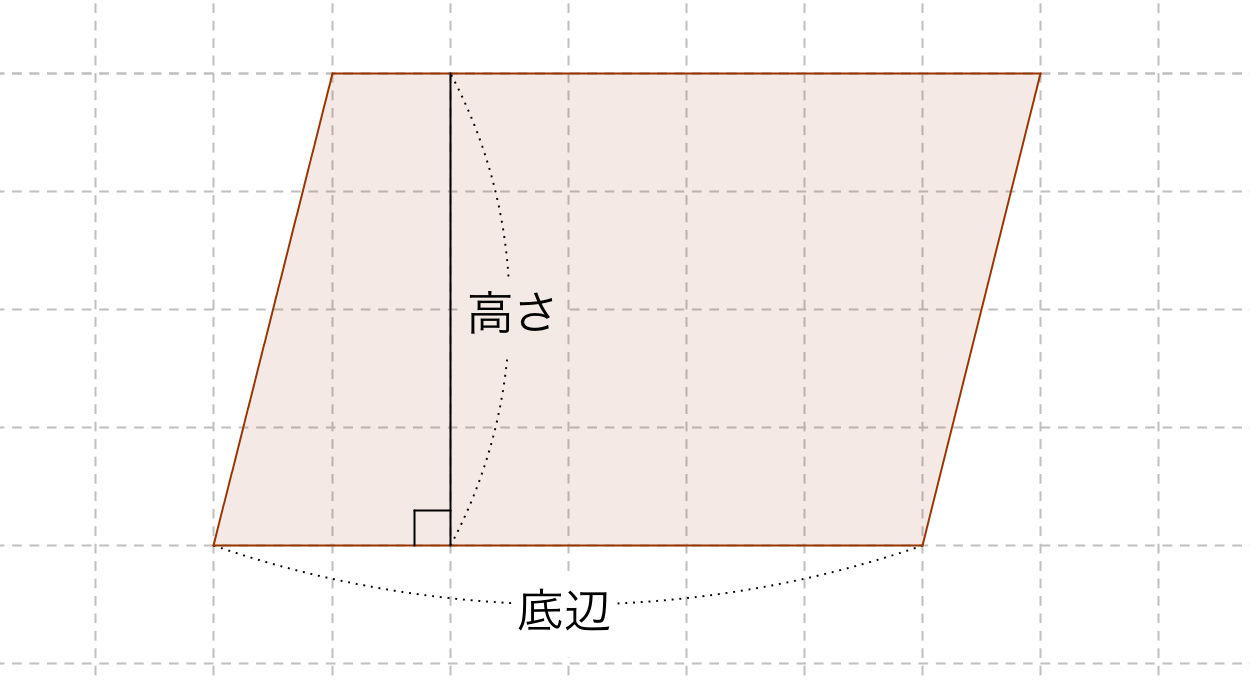
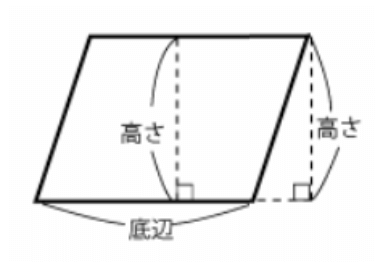
平行四辺形の面積を求める公式 面積=底辺×高さ 向き合う辺が同じ長さの四角形が平行四辺形ですが、以下のように左に直角三角形を作り、切り取って右に移動させると長方形ができます。 長方形7・平行四辺形の面積 5年 平行四辺形って? まず、平行四辺形と言うのはどういう四角形なのか、おさらい。 2組の対辺(向かい合った辺)が平行な四角形を平行四辺形と言います。参考:「その13図形の性質と集合・四角形」。 そして、覚えておいてほしい名前など。三角形 面積問題 平行四辺形 面積 図形問題 小学5年生 平行四辺形の面積もんだいは、底辺と高さを求めそれぞれを掛けるだけです すなわち 公式 底辺×高さ です 考え方は、面積のプリント①で説明してい




この問題の答えにeprqは平行四辺形とかかれていて その理由がわかりません 教えて下 Clear



平行四辺形で知っておくべきこと 苦手な数学を簡単に
よって、求めたい平行四辺形の面積は abdを2倍したものになるので 答えは160㎠ となります。 このように、平行四辺形の中にある三角形を見つけながら 相似な図形から面積比を求めたり 高さが等しい三角形から面積比を求めたりします。は長方形に変形できるという関係に着目し,平行 四辺形の面積を求める式を学習する。 本教材で扱う斜角柱の体積の求め方は,小学5 年生の平行四辺形の面積を求める学習を3次元に 拡張した内容である。平行四辺形の面積の学習で円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。 円柱の体積を求める公式



算数道場 4 面積と体積 1 面積の意味と単位 その7 平行四辺形の面積




平行四辺形の対角線の長さの求め方
6年生 Tweet 9月15日(金)1校時6年生の教室では算数の学習が行われていました。 今日は底面が平行四辺形の四角柱の体積について考えました。 最初はどうしていいか迷っている状態でしたが,平行四辺形は形を変えると長方形になることに気付き始め,解決することができていました。 そして,この立体も底面積×高さで求められることに気付いてこの長方形の面積を求めることは、平行四辺形の面積を求めることと同じ ということになります^^ 長方形の面積の求め方はもう知っていますよね? "長方形の面積=たて×よこ"です。 なので、 平行四辺形の面積=たて×よこ となるのです♪1´ ´ a¨b ∥a∥∥b∥ ¯2) " ∥a∥2∥b∥2 ´pa¨bq2 " ˆÿn i"1 a2 i ˙ˆÿn j"1 b2 j ˙ ´ ˆÿn i"1 a b ˙ˆÿn j"1 a bj ˙ " ÿn i,j"1



回転体 中学受験ー算数解き方ポータル




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
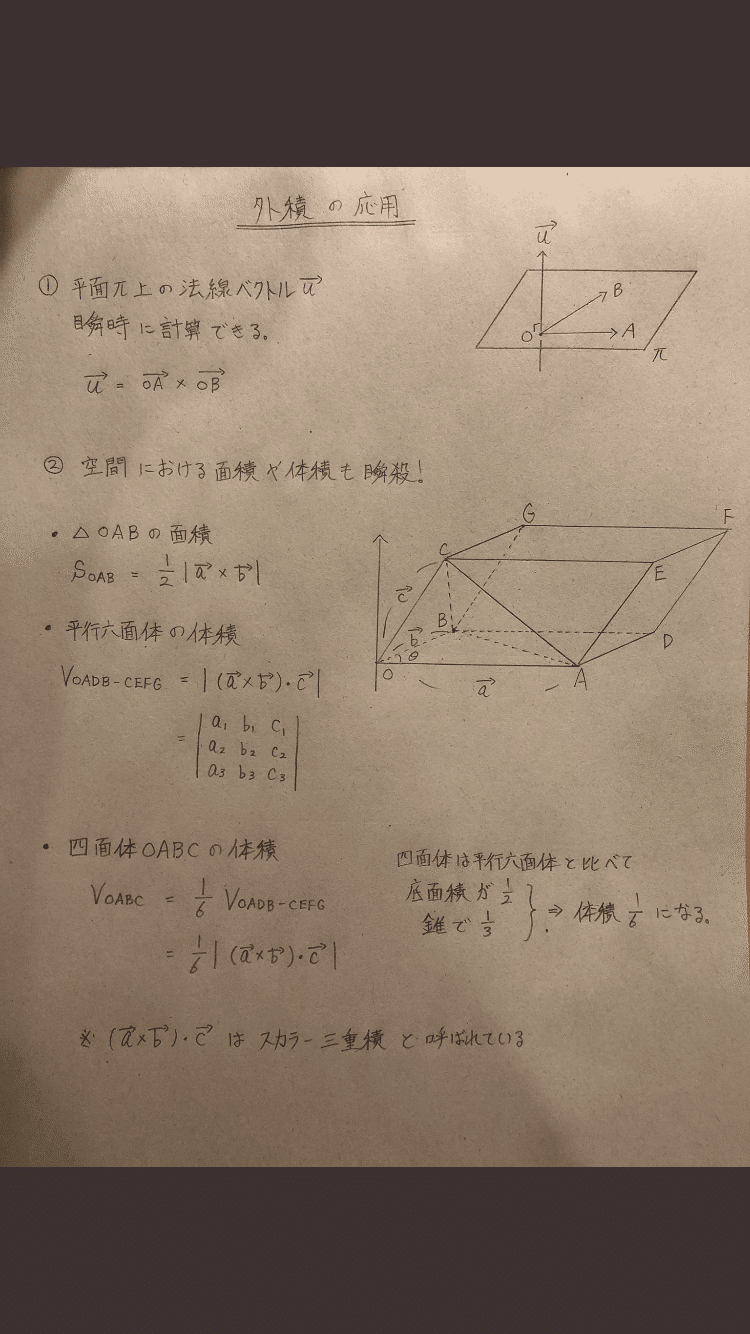
3 ベクトルの平行四辺形の面積公式 三角形oabの面積をベクトルを用いて表せたら、平行四辺形oacbの面積も簡単に導出できます。 平行四辺形の対角線を引くと、合同な三角形が 2 つ重なっている形となっています。 ですから、先に求めた、C2 とb2 の作る平行四辺形を立体の底面と見ると, b2 の終点をc2 の方向に動かしてもそ の平行四辺形の面積が変わらないので , 立体の体積も変わらない よって, a2 b2 c2 = a2 b2 c2 c2 = 1 1 0 1 3 2 1 1 2 0 B @= a3 b3 c3 とおく 1 C A 以上の変形をまとめると A = なんと, 3つのベクトルが張る平行六面体の体積は成分を並べた3×3の 行列式 として計算できるのだ ここで, 2つのベクトルが張る平行四辺形の符号付き面積が次の式で表せることを思い出そう これらはなんと美しい式ではないか! 思い返せば も も反 対称性 があったが, それは 行列式 のある行と別の行を入れ替えると符号が反転するということと対応しているのだ レヴィ・チヴィタ記




高校数学b 平行六面体と空間ベクトルの演算 受験の月




数学質問 平行四辺形を回転させてできる立体 Youtube
四角錐の底面は、長方形や平行四辺形など、どんな四角形でも 1/3 Sh で体積を求められます。 導出方法 立方体を区切って、以下のように、6つの四角錐を作ります。四角錐の体積を1とすると、立方体の体積は6です。 この立方体を半分に切ります。平行六面体OADB-CEFGの体積を求める事を考えてみた。 平行六面体の体積=底面積(平行四辺形OADBの面積)× 高さ であるから、底面積(平行四辺形OADBの面積)を求めるのに、前回の②の方法を使う。すなわち、 を利用する。2 面積・体積と行列式 2 つの平面ベクトルa = (a1 a2), b = (b1 b2) に対し, a;b の張る平行四辺形の「符 号つき」面積S(a;b) を次のように定める S(a;b) = (平行四辺形の面積), 正負の符号はa;b の位置関係―右手系をなすか左手系をなすか―により決める1




面積比と体積比 教遊者



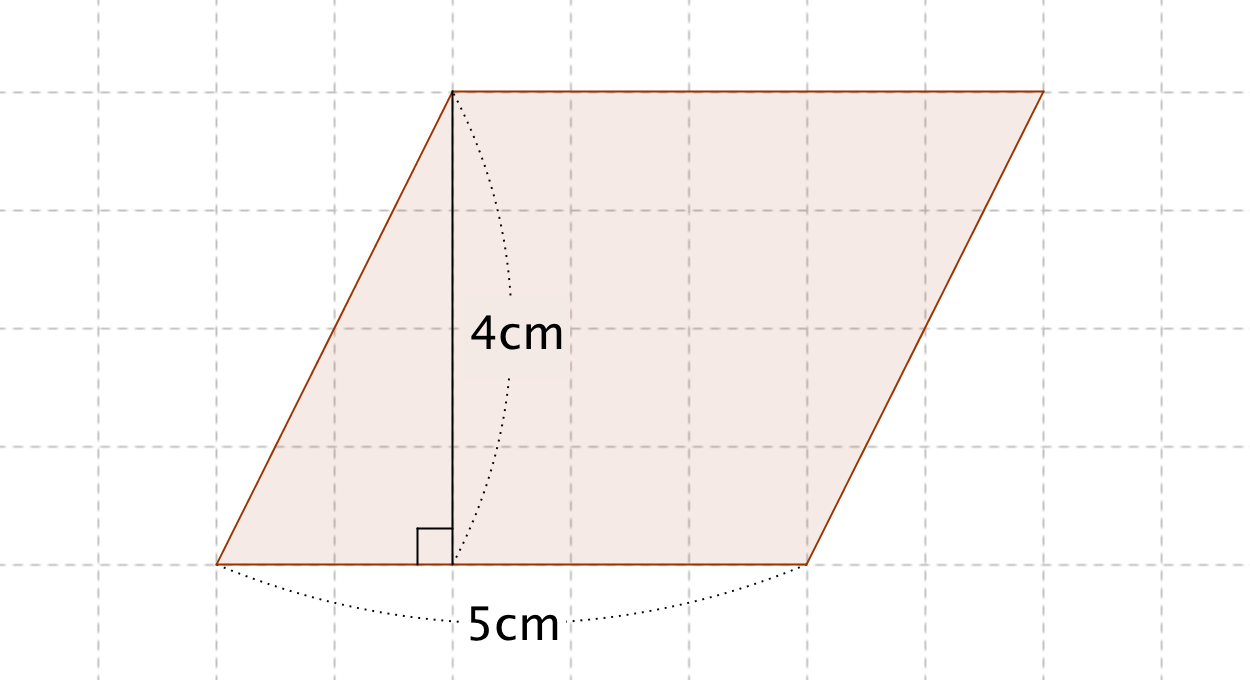
H21面積
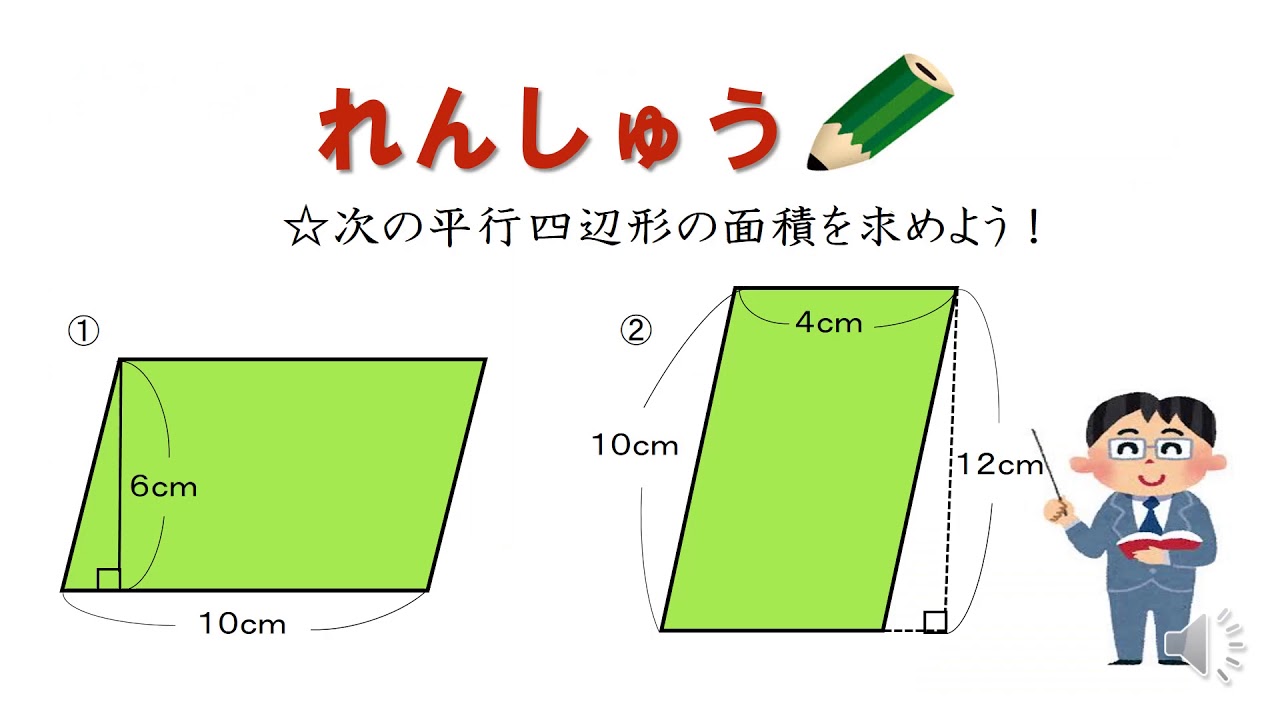
ひし形が平行四辺形であるから なんだ。 ※詳しくはひし形の定義をみてね^^ 平行四辺形の面積は「底辺×高さ」で求められたよね?? 菱形は平行四辺形ともいえるから、 この面積の公式も使えちゃうってわけさ。 じゃんじゃん計算していこう!!平行四辺形の面積を求める公式は 平行四辺形の面積 = 底辺 × 高さ なので、平行四辺形の面積を S とすると S = 5 × 4 = ( c m 2) になります。 次は小数点を含む平行四辺形の面積を計算します。は、もとの平行四辺形ではどこの長さになるか を考え、底辺と高さについて理解する。 2 底辺と高さという言葉を使って平行四辺形の 面積の公式をつくる。 技 平行四辺形の面積を求める適用問題をする。 1 等積変形などを利用して、面積の求め方を




ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門



3
まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、 対角線が他の対角線の中点を通る 平方四辺形を構成する4つの三角形の面積は等しい はかせちゃん はかせもとうとう高校数学デビュー お疲れ様でした~ はかせちゃん形でまとめることについても理解させる。 本単元では,第4 学年,第5 学年で学習した長方形,正方形,三角形,平行四辺形の面積や立体の 体積や第6 学年で学習した円の面積の学習で学んだことを生かし,一般化して角柱や円柱の体積を求ベクトル積の大きさは平行四辺形の面積 ここでは ベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しい ということについて説明します。 以前の説明 ではベクトル a → \overrightarrow {a} a と b → \overrightarrow {b} b が張る平行四辺形に、 そっと ∥ a → × b → ∥ \ \overrightarrow {a} \times \overrightarrow {b}\ ∥a × b ∥ と書いていました。




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
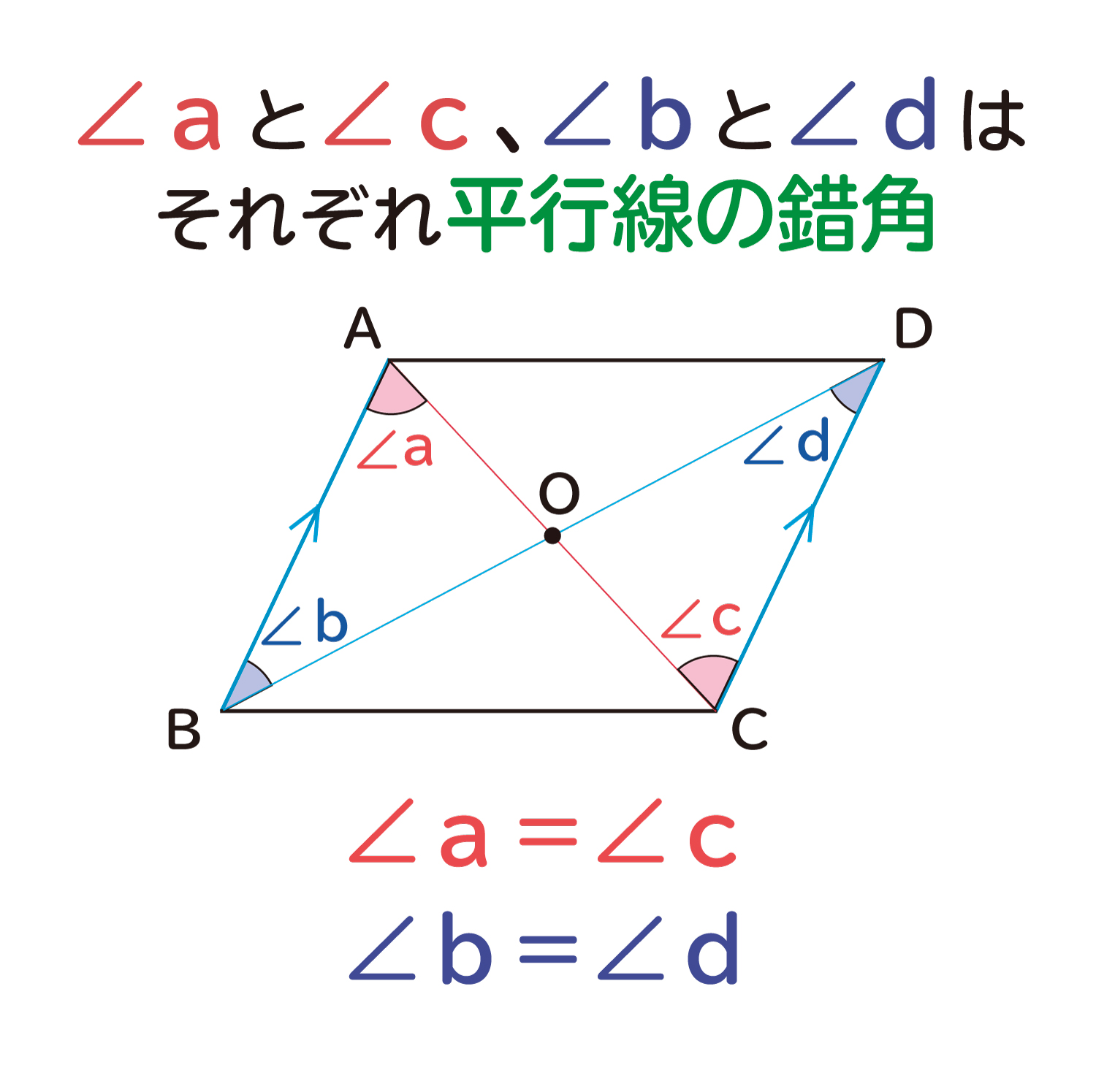



平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
立体図形を斜めに切断した時の体積は底面積×高さの平均 立体図形を斜めに切断した時の体積は底面積×高さの平均 下の図は、底面が平行四辺形の四角柱を斜めに切断したものです。 「四角柱(正方形、平行四辺形、長方形、ひし形)を斜めに切断」よって求める体積Vは, V=V 1 -V A -V B =128π/3-2×16π/3= 32π cm 3 となります. これをパップス・ギュルダンの定理を用いて解いてみます. 「 断面積 」は平行四辺形の面積となるので 2×4=8 cm 2 です. 「 断面の重心 」は図3の青い点で示す平行四辺形の中心となります.重心はLが回転すると半径2cmの円を描くので, 「 断面の重心の移動距離 」は, 2×2×π=4π cm となりま・平行四辺形の面積(底辺と高さ) 底辺と高さから平行四辺形の面積を計算します。 ・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算し
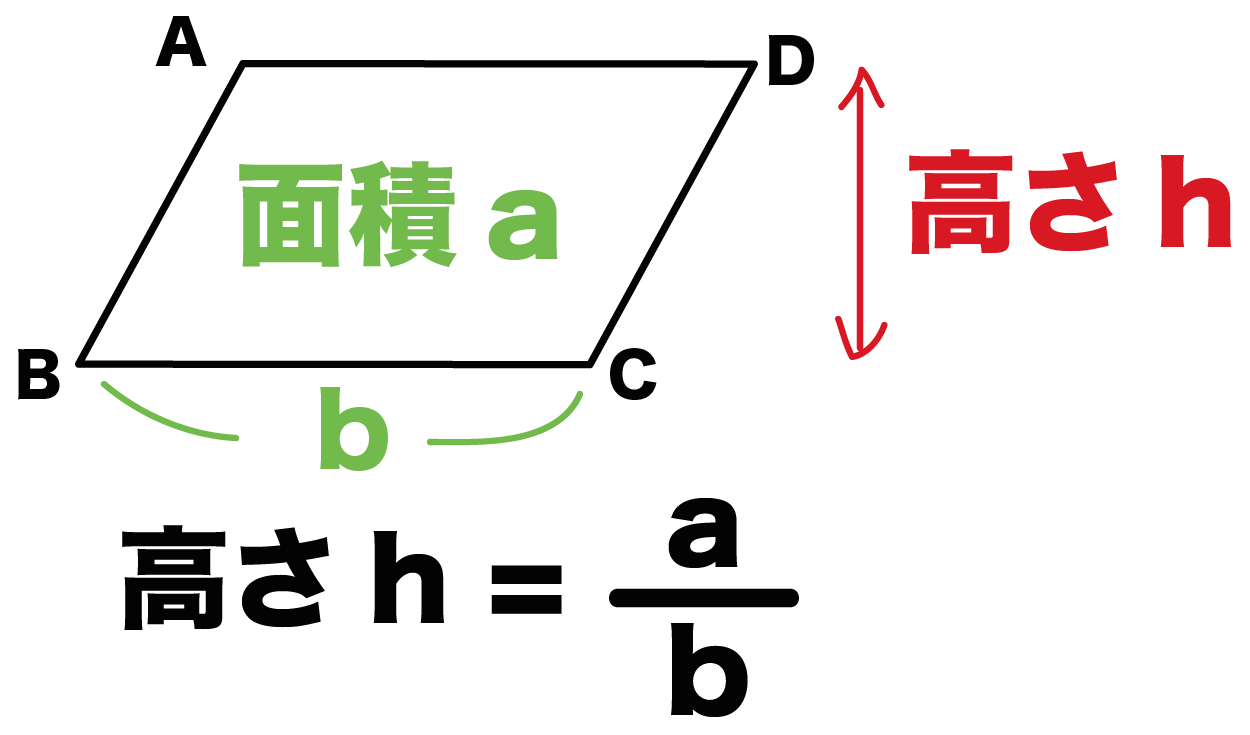



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校
平行な \(2\) つの平面を底面にもつ筒状の空間図形です。 三角柱 三角柱の体積・表面積の公式や、展開図の書き方を説明しています。 三角柱とは?体積・表面積の公式や求め方をわかりやすく解説 三角柱の展開図の作り方




立方体の切断 断頭柱体のうち 底面が円 平行四辺形 三角形のものの体積は 底面積 高さの平均 ワンセンテンス算数 Note



大妻中野中学校入試問題のポイント



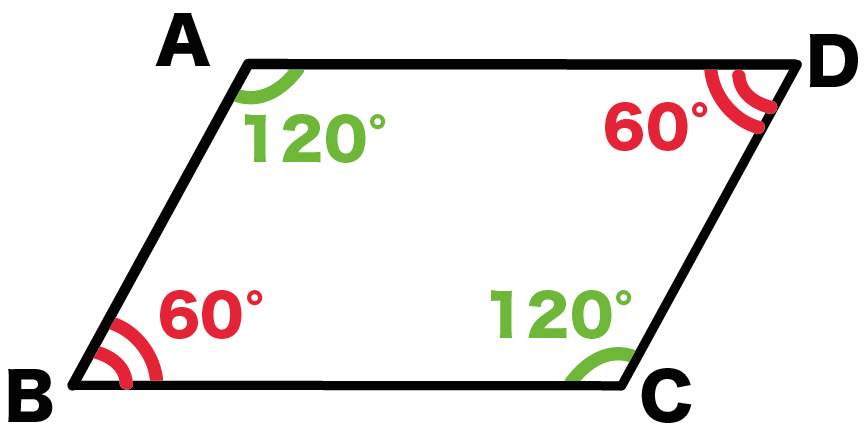
平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典




立方体の切断 断頭柱体のうち 底面が円 平行四辺形 三角形のものの体積は 底面積 高さの平均 ワンセンテンス算数 Note




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例



2



5年算数三角形と四角形の面積2 教え方 台形 ひし形



立体の体積は 2015年 大宮開成中学 どう解く 中学受験算数




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



5年 平行四辺形の面積 算数イメージ動画集 大日本図書



3




大学入試過去問 検索結果



平行四辺形の対辺の長さは等しくなる ことの説明 おかわりドリル




黒木玄 Gen Kuroki 数楽 添付画像は 2次元の場合のクラメールの公式が 行列式が 面積 符号が 向き を表す であることから 見た目的に 明らか な公式に過ぎないことの説明 平行四辺形の変形が 向き を変えないことも明らか N次元も同様




空間図形16 直方体の切断 Youtube



立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ




小5 算数 小5 41 平行四辺形の面積 Youtube



平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典




面積 平行四辺形の面積 01 高さが外にあるときの面積の求め方 Youtube



平行四辺形の面積の公式 算数の公式




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



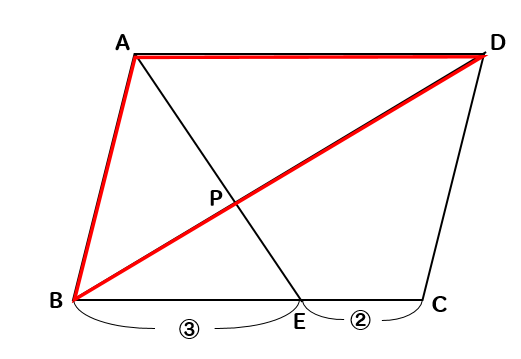
平行四辺形を分ける面積比の求め方 算数解法の極意




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




Maya Script 試行錯誤



平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット
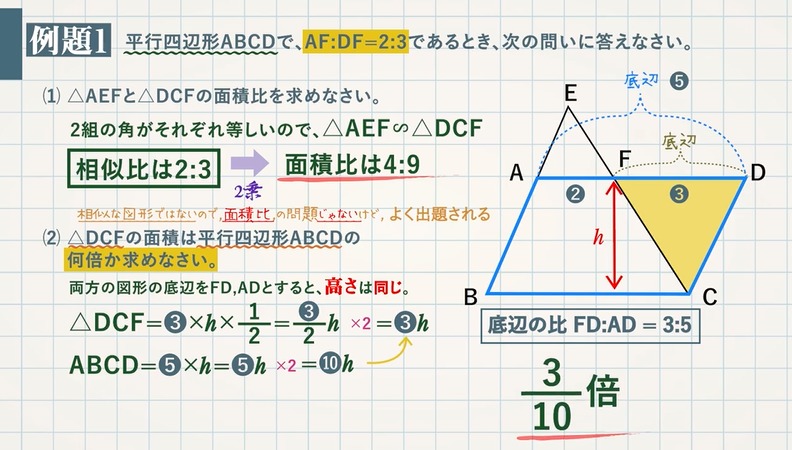



面積比と体積比 教遊者




平行四辺形の面積の求め方 公式と計算例




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




空間の幾何学 解法まとめ 数検1級対策 Note



第81問の解答
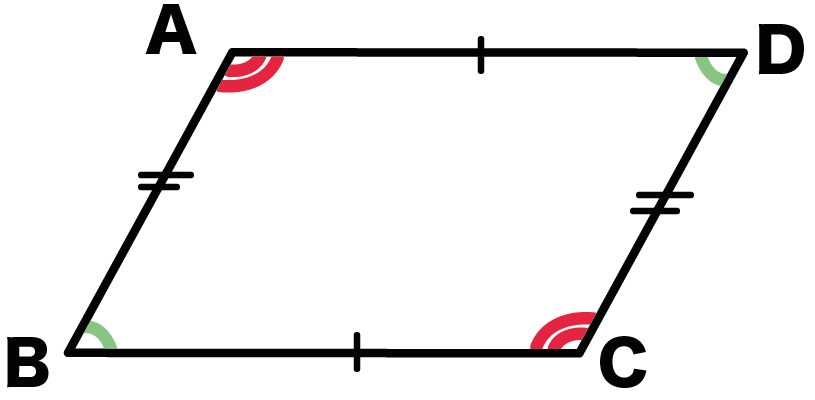



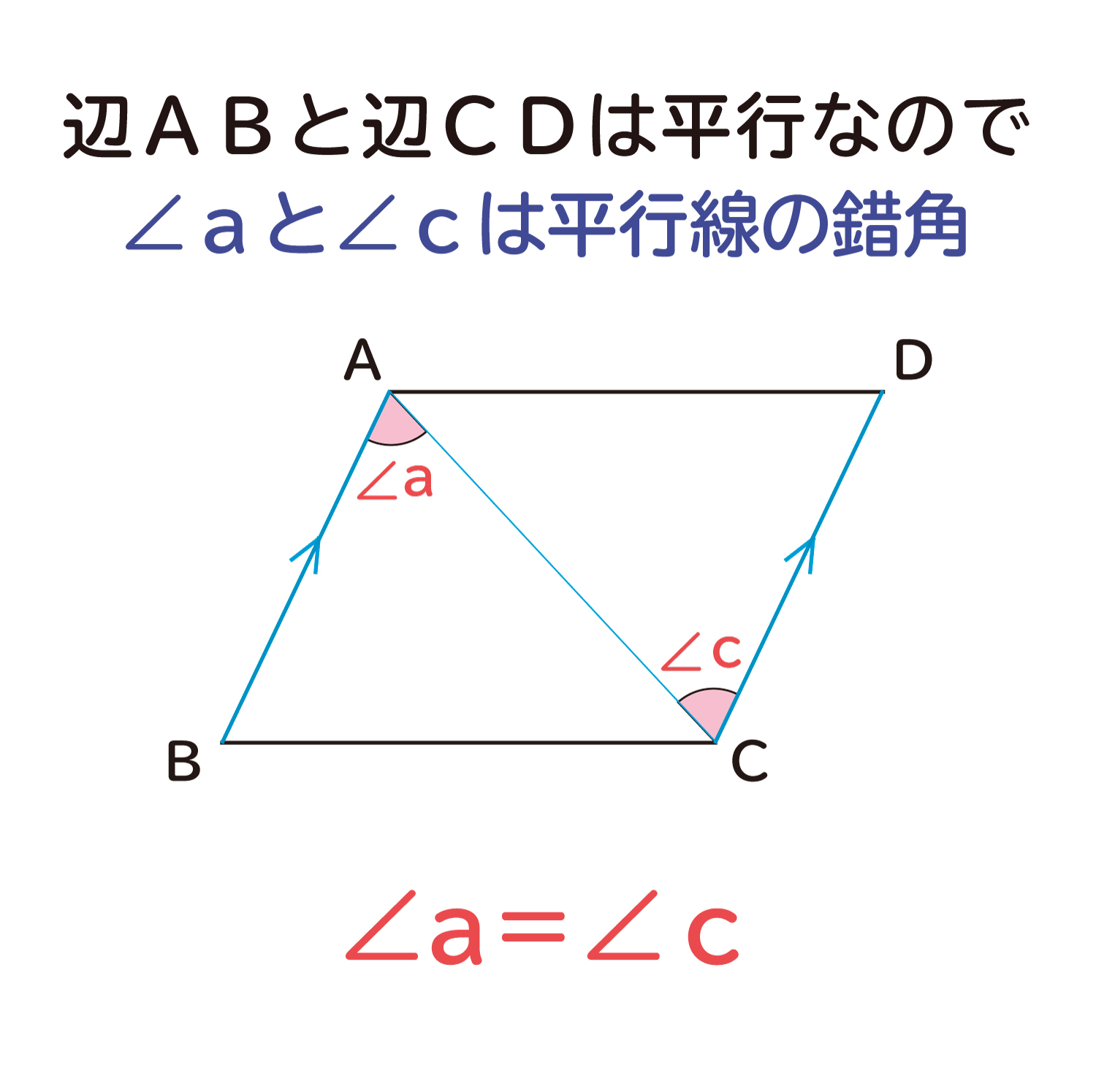
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



立体の体積 理数系学習サイト Kori



平行四辺形の面積の公式 算数の公式




平行四辺形の面積の求め方 公式と計算例



回転体 中学受験ー算数解き方ポータル



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



大至急 底面が平行四辺形である四角柱 正四角錐の表面積の解き方 Yahoo 知恵袋



立体の体積は平行線でね 基本に忠実に本質を伝える 楽天ブログ



回転体 中学受験ー算数解き方ポータル



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく




底面が平行四辺形の四角柱の体積について考えました 6年算数 茎崎学園 つくば市立茎崎第二小学校



17年2月号の巻 難攻不落の算数城攻略 忍者エピス丸 Epis Education Centre Epis Education Centre
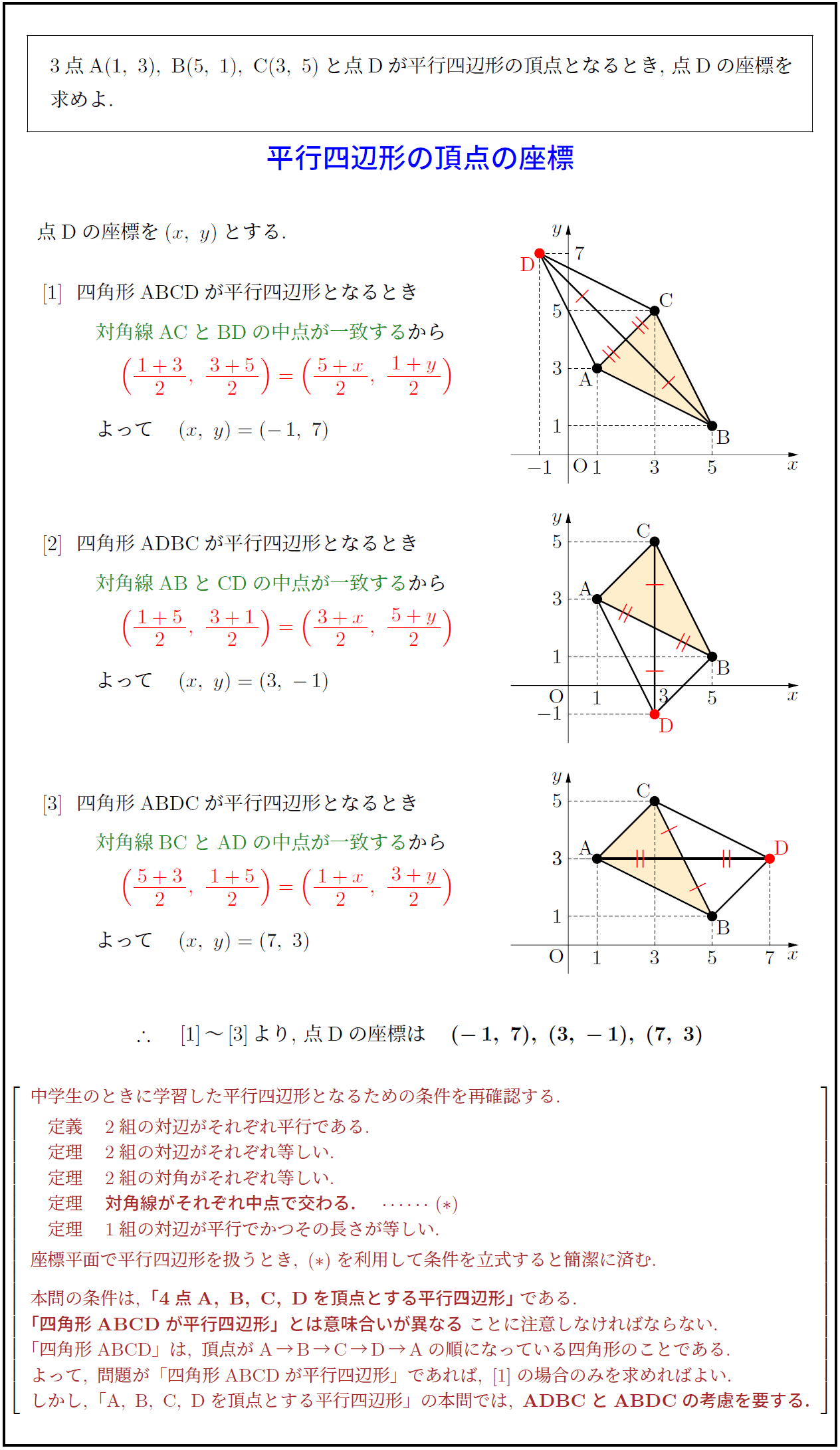



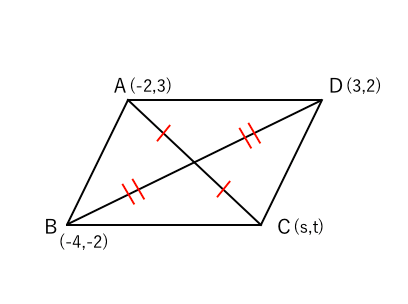
高校数学 平行四辺形の頂点の座標 受験の月
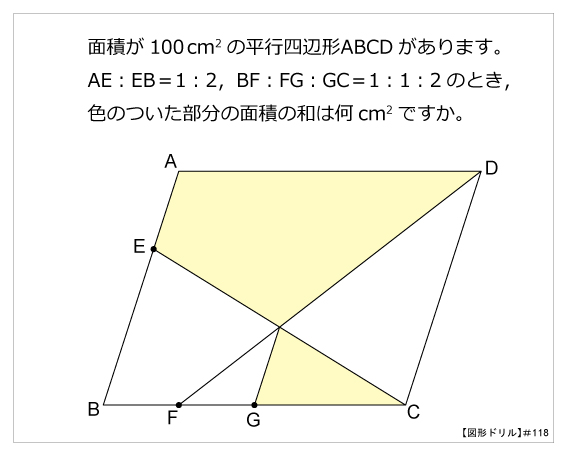



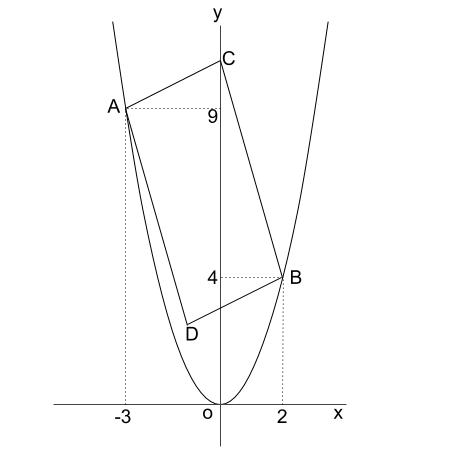
第118問 平行四辺形の面積の和 図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦



平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典




高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月



2
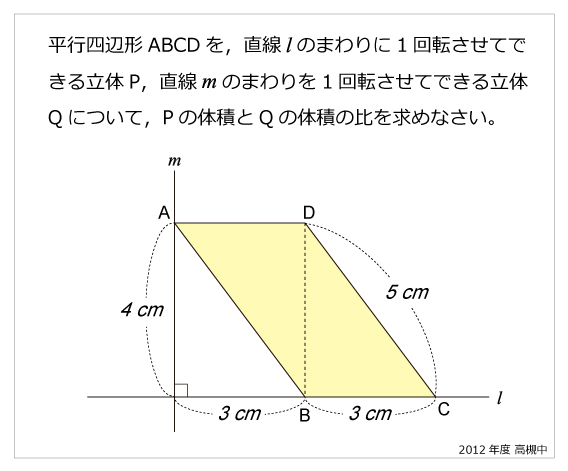



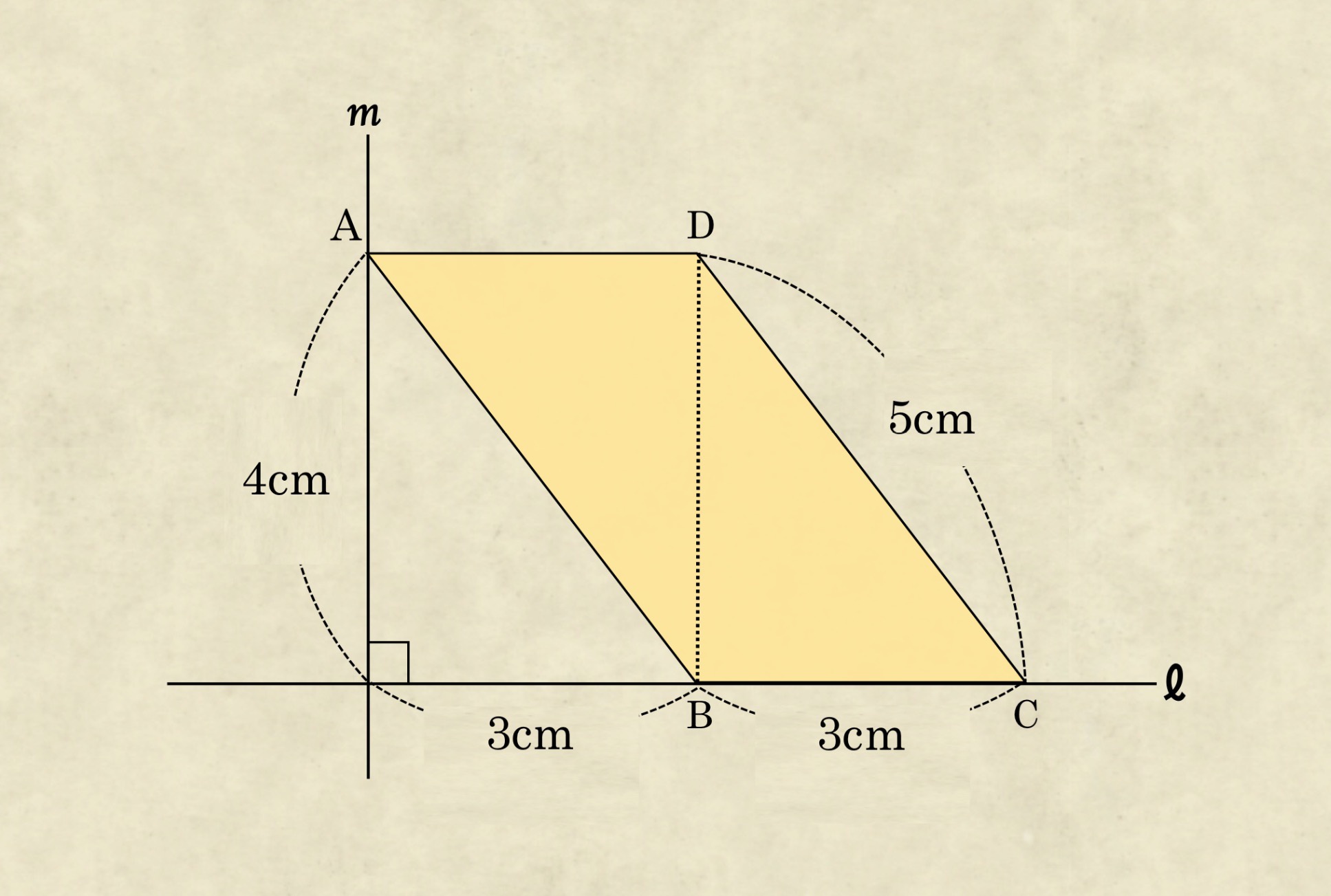
高槻中 パップス ギュルダン12年高槻中 パップス ギュルダン 算数星人のweb問題集 中学受験算数の問題に挑戦
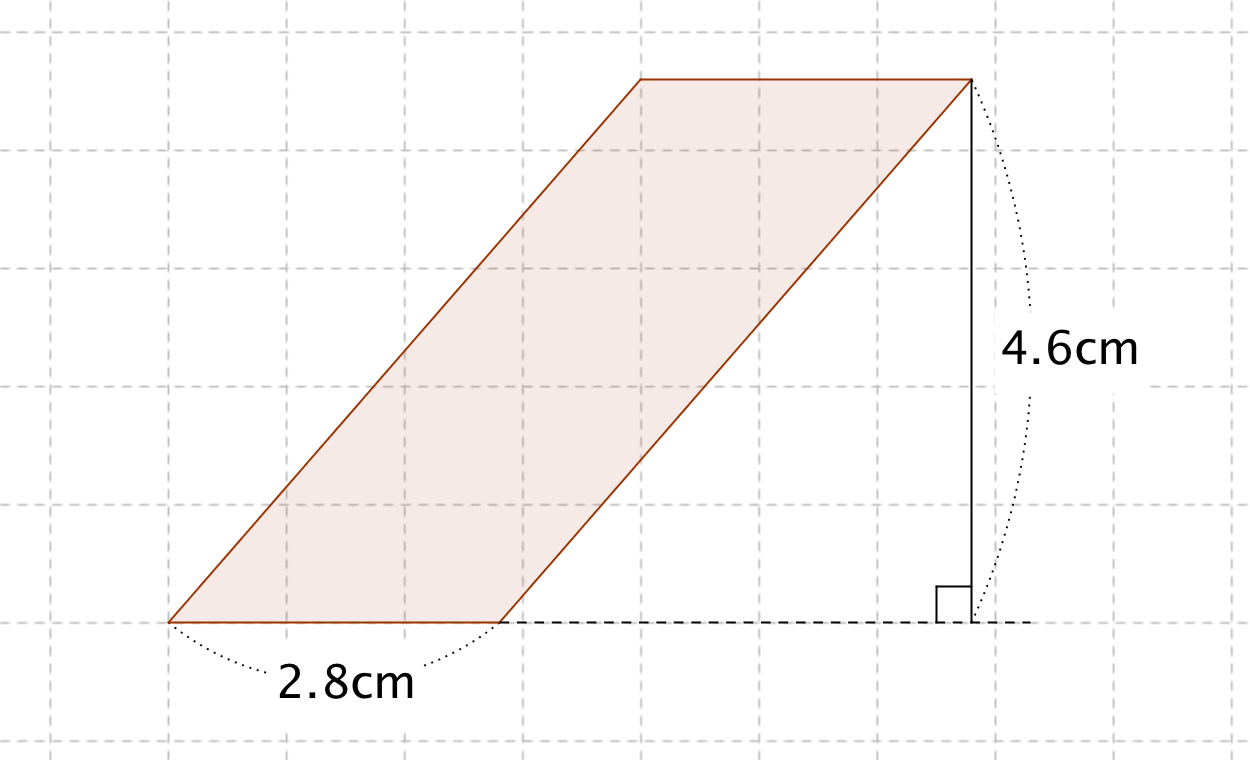



平行四辺形の面積の公式 算数の公式
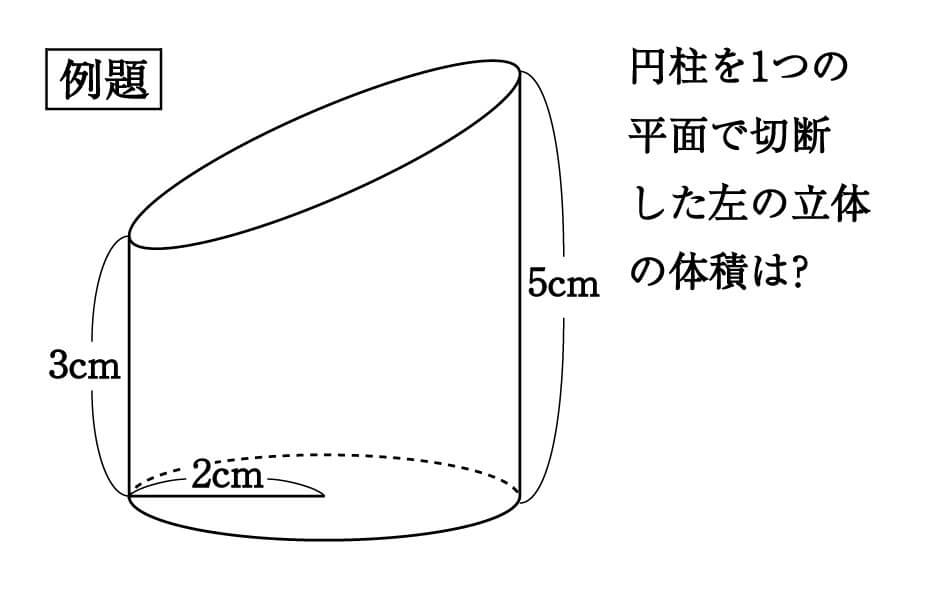



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
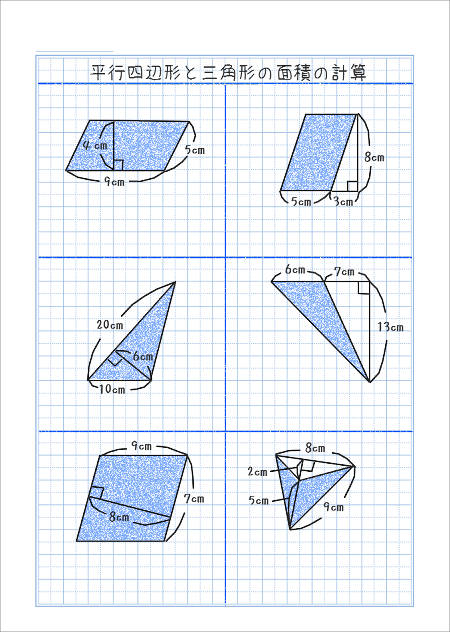



平行四辺形と三角形の面積 家庭学習レシピ
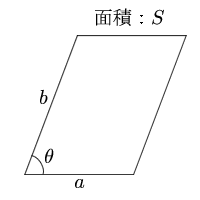



平行四辺形 2辺と間の角度 面積の計算 計算サイト
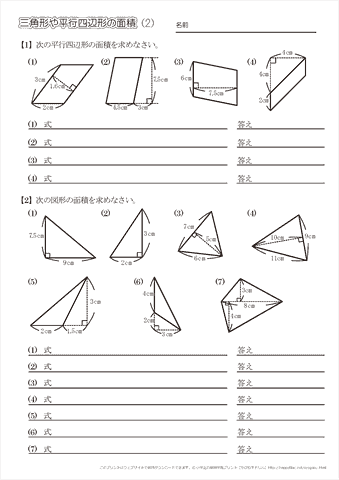



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



第81問の解答



2




平行四辺形の面積の求め方 公式と計算例
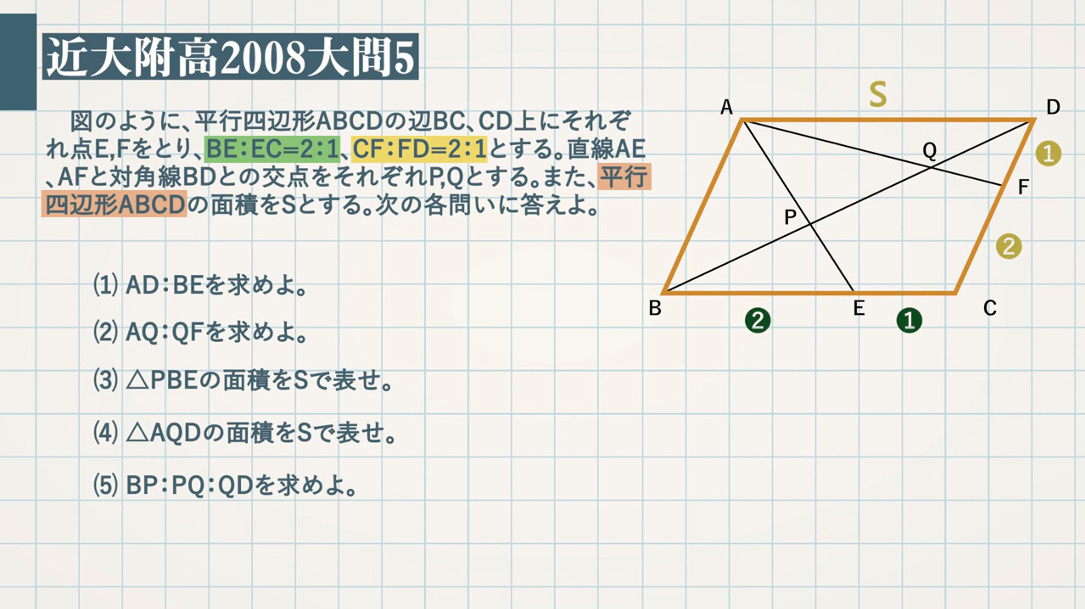



平行四辺形と比 教遊者




平行四辺形の面積の求め方 公式と計算例
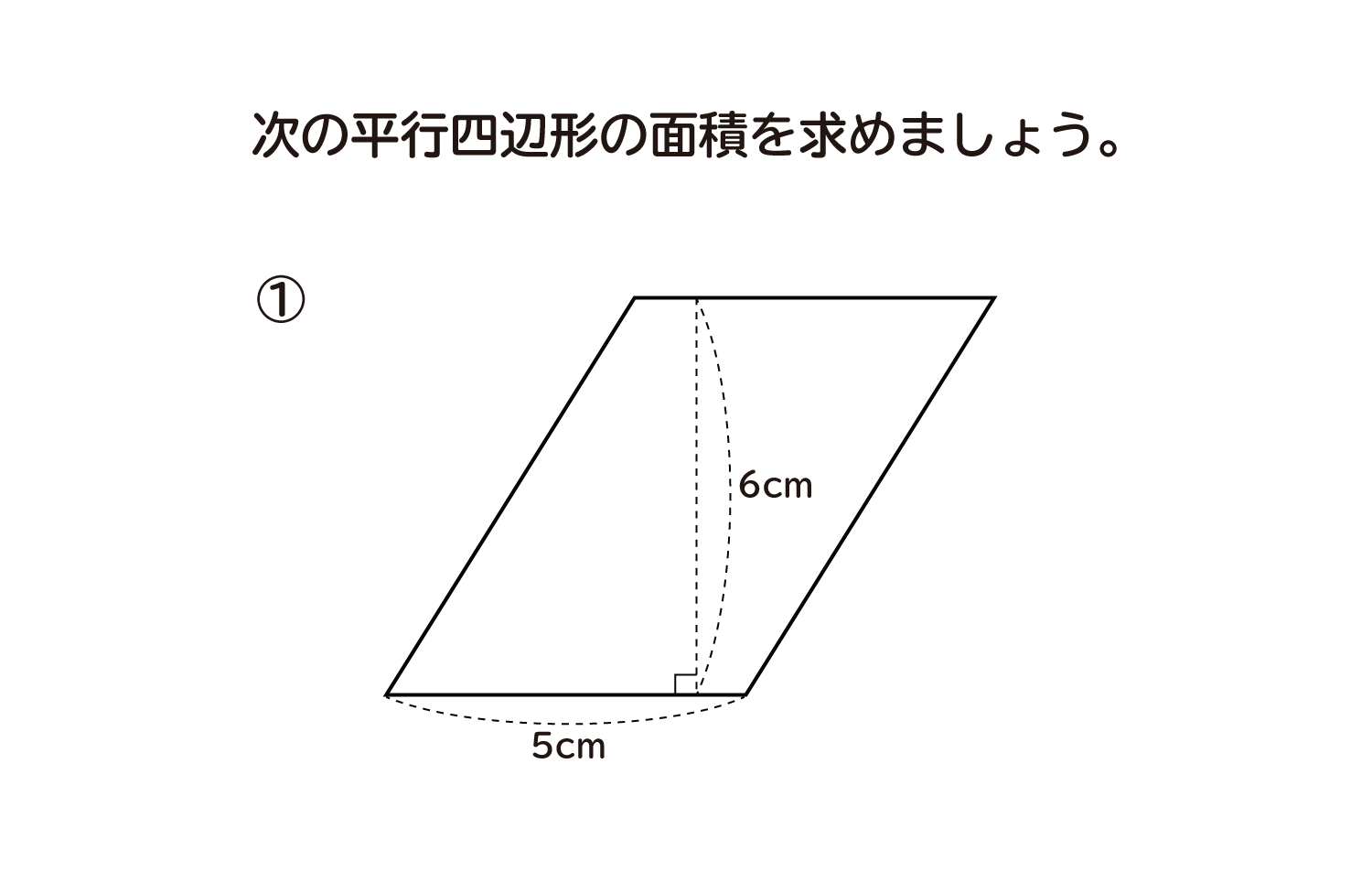



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル
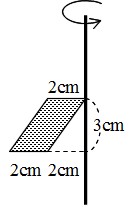



Math 回転体の体積 表面積とパップス ギュルダンの定理 働きアリ



図形の回転 第2問 ラ サール中学 入試算数問題 類題 浅野中学 03年 入試算数問題 類題 まいにち一題 中学受験過去問題研究




回るとどうなる 回転体の 体積 名寄 算数数学教室より




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット



回るとどうなる 回転体の 体積 名寄 算数数学教室より



2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




塾 学校 家庭を結ぶ 受験情報サイト 学びネット



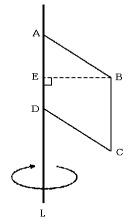
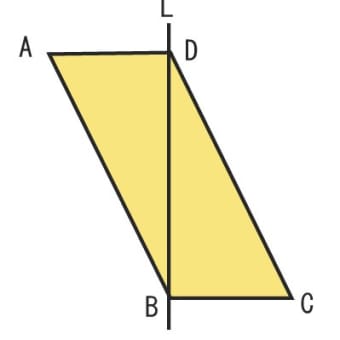
教えてください 図のような平行四辺形abcdを直線lを軸として1回転させ Yahoo 知恵袋



平行四辺形が回転すると 高槻中学 12年 中学受験ー算数解き方ポータル



相似 平行四辺形と面積比の問題を徹底解説 数スタ



小5 面積の求め方を考えよう 平行四辺形 日本語版 Youtube




モデルの体積を計算する 試行錯誤



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 中学生




面積比 Youtube
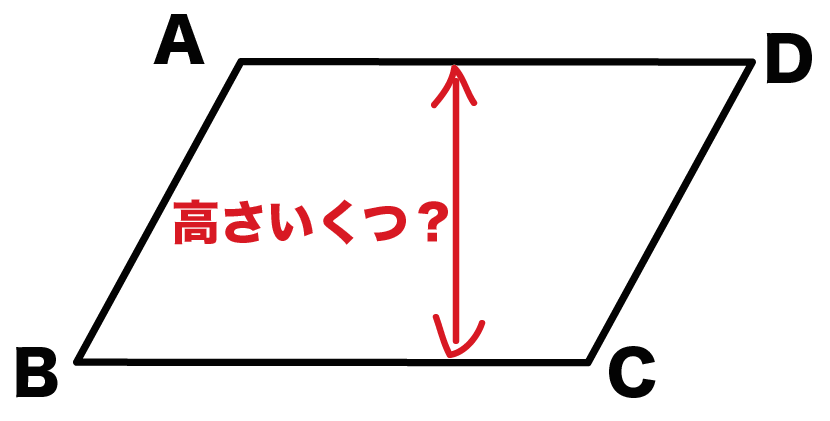



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく
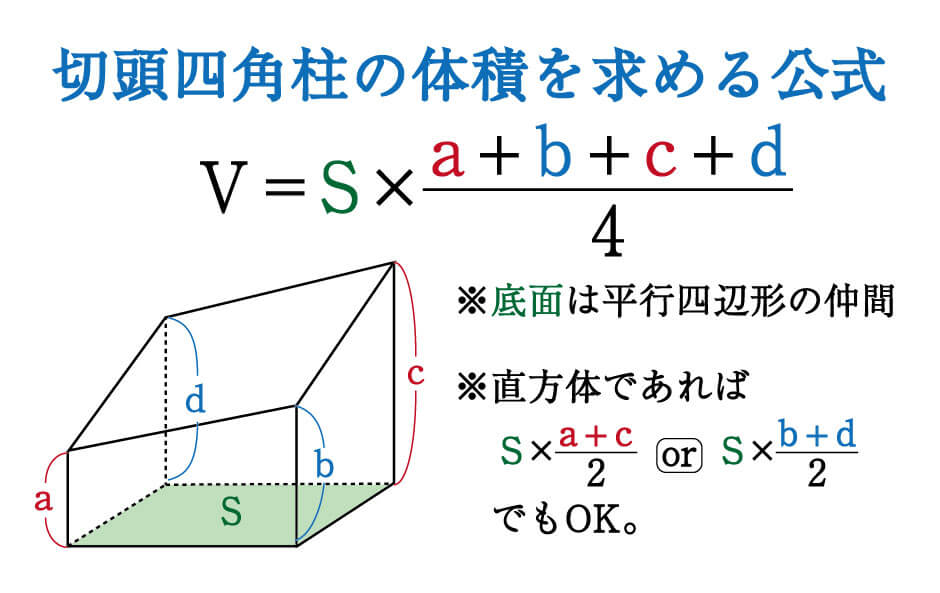



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
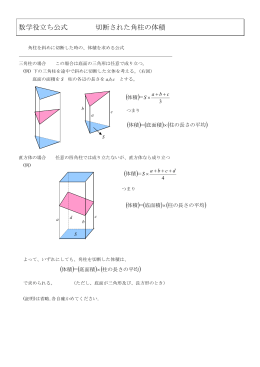



角柱の体積 底面積 高さ 平行四辺形の面積 底辺 高さ 台形の面積



1
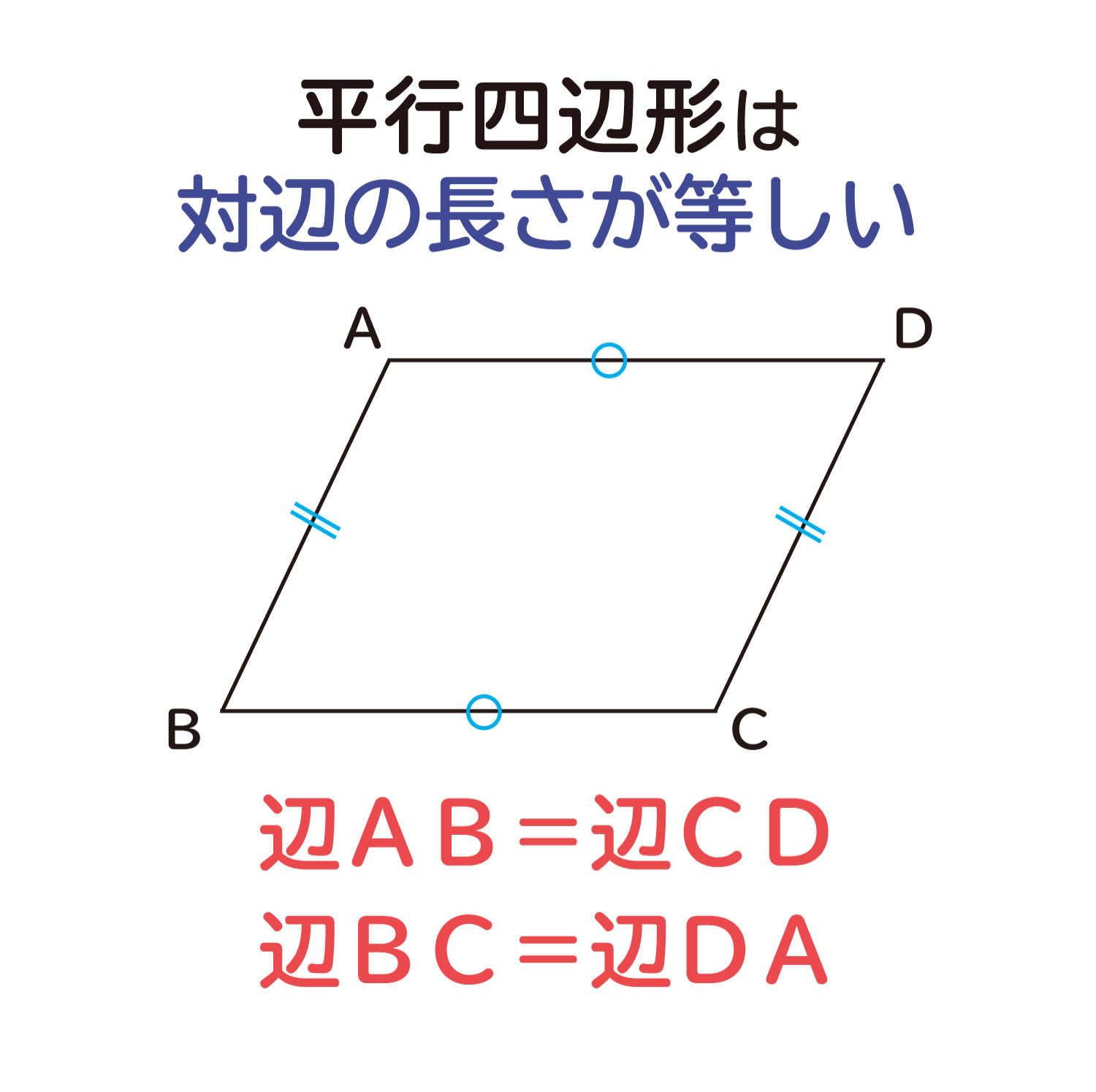



平行四辺形の対辺の長さは等しくなる ことの説明 おかわりドリル



1
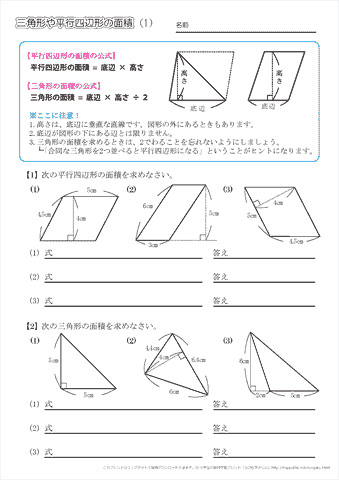



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
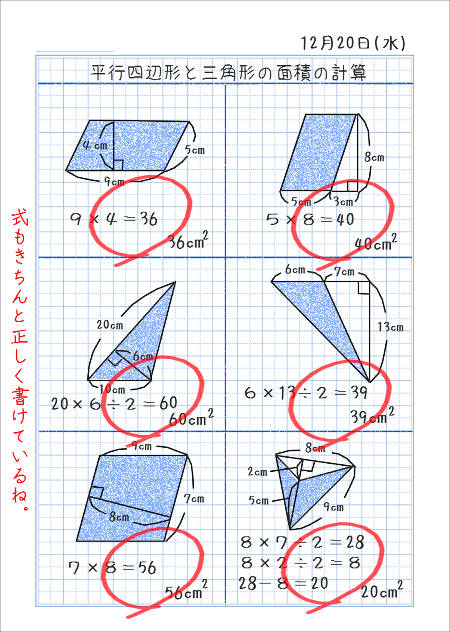



平行四辺形と三角形の面積 家庭学習レシピ
コメント
コメントを投稿